

The book is an ideal reference for scientists in biomedical and genomics research fields who analyze DNA microarrays and protein array data, as well as statisticians and bioinformatics practitioners. Utilizing research and experience from highly-qualified authors in fields of data analysis, Exploration and Analysis of DNA Microarray and Other High-Dimensional Data, Second Edition features:Ī new chapter on the interpretation of findings that includes a discussion of signatures and material on gene set analysis, including network analysis New topics of coverage including ABC clustering, biclustering, partial least squares, penalized methods, ensemble methods, and enriched ensemble methods Updated exercises to deepen knowledge of the presented material and provide readers with resources for further study The new edition answers the need for an efficient outline of all phases of this revolutionary analytical technique, from preprocessing to the analysis stage. A cutting-edge guide, the Second Edition demonstrates various methodologies for analyzing data in biomedical research and offers an overview of the modern techniques used in microarray technology to study patterns of gene activity.

Most of the concepts studied and presented in this thesis are illustrated on chemometric data, and more particularly on spectral data, with the objective of inferring a physical or chemical property of a material by analysis the spectrum of the light it reflects.“…extremely well written…a comprehensive and up-to-date overview of this important field.” – Journal of Environmental QualityĮxploration and Analysis of DNA Microarray and Other High-Dimensional Data, Second Edition provides comprehensive coverage of recent advancements in microarray data analysis.
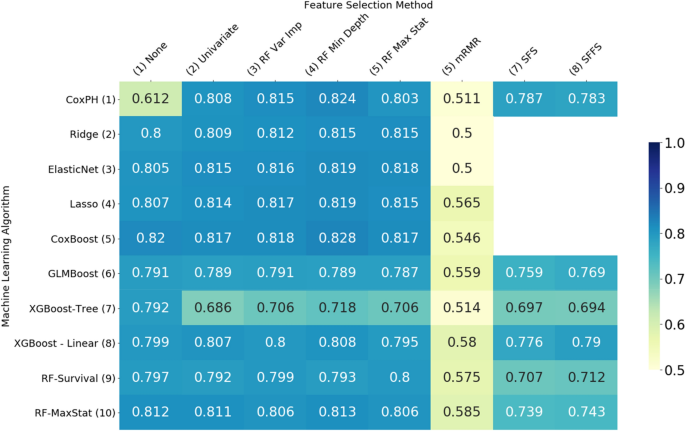
#High dimensional data analysis methods pdf#
Two methods are proposed to (1) reduce the computational burden of feature selection process and (2) cope with the instability induced by high correlation between features that often appear with high-dimensional data. Request PDF Assessing Normality of High-Dimensional Data The assumption of normality is crucial in many multivariate inference methods and may be even more important when the dimension of data. Part Two of this thesis focuses on the problem of feature selection in the case of a large number of initial features. Data on health status of patients can be high-dimensional (100+ measured/recorded parameters from blood analysis, immune system status, genetic background, nutrition, alcohol- tobacco- drug. It is shown that for nearest neighbours search, the Euclidean distance and the Gaussian kernel, both heavily used, may not be appropriate it is thus proposed to use Fractional metrics and Generalised Gaussian kernels. In Part One of the thesis, the phenomenon of the concentration of the distances is considered, and its consequences on data analysis tools are studied. Computational aspects, randomized algorithms.

Clustering, classification and regression in high-dimensions. Random walks on graphs, diffusions, page rank. Nonlinear dimension reduction, manifold models. This thesis therefore focuses the choice of a relevant distance function to compare high-dimensional data and the selection of the relevant attributes. Linear dimension reduction, principal component analysis, kernel methods. The Euclidean distance is furthermore incapable of identifying important attributes from irrelevant ones. But the Euclidean distance concentrates in high-dimensional spaces: all distances between data elements seem identical. For example, a dataset that has p 6 features and only N 3 observations would be considered high dimensional data because the number of features is larger than the number of observations. For instance, many tools rely on the Euclidean distance, to compare data elements. High dimensional data refers to a dataset in which the number of features p is larger than the number of observations N, often written as p > N. Many of the explicit or implicit assumptions made while developing the classical data analysis tools are not transposable to high-dimensional data. However, many data analysis tools at disposal (coming from statistics, artificial intelligence, etc.) were designed for low-dimensional data. The development leverages a range of physics and learning based approaches, including nonlinear wave simulations (potential flow), ship response simulations (e.g., CFD), dimension-reduction techniques, sequential sampling, Gaussian process regression (Kriging) and multi-fidelity methods. The Little Book of Fundamental Indicators: Hands-On Market Analysis with Python: Find. are described by thousands of attributes. Reducing High Dimensional Data with PCA and prcomp: ML with R. High-dimensional data are everywhere: texts, sounds, spectra, images, etc.


 0 kommentar(er)
0 kommentar(er)
